Один из идеалов оригами требует складывания исходного квадрата без предварительных чертежей и измерений. При таком складывании возникает проблема в случае, если необходимо сложить лист бумаги, например, втрое. Как это сделать, не прибегая к карандашу? В данной статье рассматривается вопрос деления квадратного листа бумаги на две, три, четыре, ... десять равных частей.

Деление листа бумаги на две части не представляет сложности, поскольку реализуется просто складыванием базовой формы книжка. Перейдем к более сложной задаче деления квадратного листа на три части.

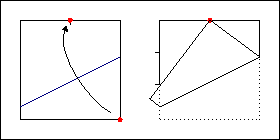
Эта задача уже не столь проста. Для ее решения нам потребуется теорема Хага. Сложим угол квадрата к середине противоположной стороны. В таком случае точка пересечения другой стороны, противоположной этому углу и стороны, прилегающей к нему делит сторону в отношении один к двум. Таким образом, с помощью только складок мы нашли треть стороны квадрата.

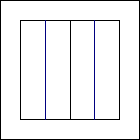
Следующая задача - деление стороны квадрата на четыре равные части. Для этого достаточно их поделить пополам, а затем, каждую из половинок снова пополам. Именно так происходит, когда мы складываем базовую форму дверь.

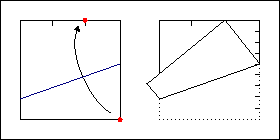
Как легко догадаться, деление квадрата на пять частей с помощью складывания представляем собой гораздо более сложную задачу. Ее решение изображено на рисунке. Попробуйте сами доказать, что таким образом мы действительно разделим квадрат именно на пять частей. Через некоторое время я приведу доказательство этой теоремы.

Для того чтобы разделить сторону квадрата на шесть частей, нам достаточно разделить ее на три части, как было показано ранее. А, затем, каждую из частей разделить пополам.

Можно заметить, что особые сложности вызывает деление квадрата на количество частей, являющееся простым числом. Приступим к делению стороны на семь одинаковых частей. Для этого сначала разделим квадрат на пять равных частей, а затем, сделаем действие, изображенное на картинке.

Поделить квадрат на восемь равных частей совсем просто. Для этого достаточно поделить его на четыре равные части, а затем, каждую из них разделить еще пополам.

Для деления на девять равных частей можно предложить два способа. Первый из них заключается в том, чтобы разделить сначала на три равные части, а потом повторить деление на три для маленького квадрата. Однако этот способ плох тем, что при его применении на практике трудно будет соблюсти достаточную точность, поскольку погрешности, совершенные на разных этапах складываются.

Другой способ более оригинален и основан на развитии теоремы Хага, которое предложили Коджи и Мицуе Фушими. Заметим, что этот способ применялся при делении квадрата на семь и девять частей. Может быть он применим и для деления его на девять частей?

И, наконец, деление на десять частей представляет собой последовательное деление на пять частей, а затем деление пополам каждой из пяти частей.